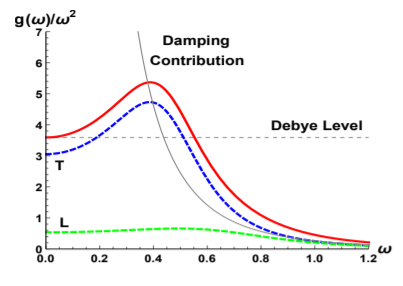
The vibrational spectra of solids, both ordered and amorphous, in the low-energy regime, control the thermal and transport properties of materials, from heat capacity to heat conduction, electronphonon couplings, conventional superconductivity etc. The old Debye model of vibrational spectra at low energy gives the vibrational density of states (VDOS) as proportional to the frequency squared, but in many materials the spectrum departs from this law which results in a peak upon normalizing the VDOS by frequency squared, which is known as the “boson peak”. A description of the VDOS of solids (both crystals and glasses) is presented starting from first principles. Without using any assumptions whatsoever of disorder in the material, it is shown that the boson peak in the VDOS of both ordered crystals and glasses arises naturally from the competition between elastic mode propagation and diffusive damping. The theory explains the recent experimental observations of boson peak in perfectly ordered crystals, which cannot be explained based on previous theoretical frameworks. The theory also explains, for the first time, how the vibrational spectrum changes with the atomic density of the solid, and explains recent experimental observations of this effect.
