Karl Landsteiner

Quantum Field Theory

is the most fundamental mathematical concept to describe nature. It describes the quantum behavior of (infinitely) many particles interacting with according to the laws of quantum theory. In high energy physics due to the underlying Lorentz symmetry quantum field theory is enforced on us because energy can be converted to particles via Einsteins famous relation $E=mc2$. Quantum field theory combines this with Planck's formula $E=h\nu$ (the most important equation in modern physics). Therefore we are always dealing with fields and view particles as quanta of the fundamental fields. But quantum field theory also applies in many other situations without Lorentz invariance and in the recent years it has become of ever greater importance in the description of exotic new quantum states of matter such a topological insulators and topological semi-metals.

The Holographic Duality

also known as gauge/gravity duality is an idea which has its origins in string theory. In its original form it states that string theory on a five-dimensional anti de-Sitter space (and an internal five-dimensional sphere) is exactly the same as maximally supersymmetry gauge theory in four dimensions. More generally it maps a gravitational theory to a quantum field theory in one dimension less. This change in dimenions is what makes it holographic. Indeed this holographic principle is thought to be a fundamental property of quantum gravity. On the other hand one can use the gravity theory to compute expectation values and correlation functions of local operators (observables) in the dual quantum field theory. This becomes especially interesting for my research if one considers black holes in asymptotically ant de-Sitter spaces. The dual quantum field theory is then heated up to a temperature which is equivalent to the Hawking temperature of the black hole. This has led to important new insights into the behavior of quantum field theories at finite temperature. In particular the modern understanding of such an old subject as hydrodynamics is based on this duality!

Quark Gluon Plasma

is the state of nuclear matter when it is heated up to an extreme temperature of around $$5x10¹²degrees. The universe approximately one microsecond after the big bang was filled with this type of matter. It can be created at present on earth in experiments of heavy ion collisions at the Relativistic Heavy Ion Collider (RHIC) in Brookhaven USA and the Large Hadron Collider (LHC) at CERN, Geneva, Switzerland. The basic building blocks of all nuclear matter are quarks and gluons. At everyday energies they are confined within protons and neutrons. But at high temperature a new state of matter is formed in which quarks and gluons are deconfined. Experimental results indicate that this state of matter is behaving like a strongly coupled fluid with no quasiparticle excitations. Such strongly coupled quark gluon plasmas can effectively be modelled by the holographic duality via black holes in anti de-Sitter space.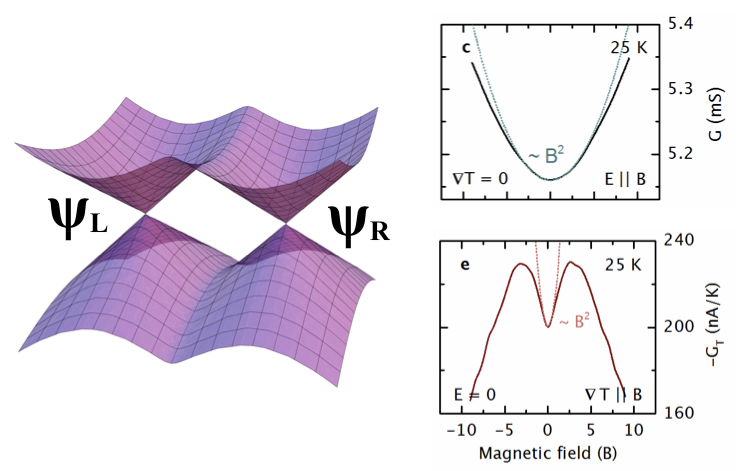

Condensed Matter Physics

It is very interesting that modern condensed matter physics uses more and more concepts form quantum field thery and high energy physics. This is especially true for the theory of topological quantum matter. I am particularily interesting in the physics of Weyl and Dirac (semi-)metals. These are advanced types of materials in which the electrons move not according to the non-relativistic Schrödinger equation but according to the relativistic Dirac equation. The electronic quasiparticles in these materials behave effectively like relativistic chiral fermions. This allows to apply relativistic quantum field theory and in particular the theory of anomalies and anomalous transport to the electronics of these new type of materials. Weyl semimetals allow to successfully test the theory of anomaly induced transport phenomena in table top experiments and predicted phenomena such a strong enhancement of electric conductivity along a magnetic field have indeed been measured!