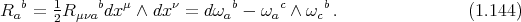1 Differential Geometry

Chapter 1
Differential Geometry

Page 7, Eq. (1.27): a vertical bar between the subindices λ and ν in the second term is missing (the antisymmetrization affects only μ and ν):

R μνρσ(Γ ) = 2∂[μΓ ν]ρσ + 2 Γ [μ|λσΓ |ν]ρλ . (1.27)

Page 8, Eq. (1.34): there is a term missing in the r.h.s.:

R = 1 *∇ *T ρ + 1R ρ . (1.34) [μν] 2 ρ μν 2 μνρ

The missing term vanishes for metric-compatible connections. (Thanks to Bert Janssen for pointing this missprint to us.)

Page 8, Eq. (1.37): ϵ should be ξ and two indices in the last term should be interchanged

ρ ( λ ρ) ( λ ρ) ( ρ λ) λ ρ σ ρ L ξTμν = ∇ μ ξ T λν + ∇ ν ξ T μλ - ∇ λ ξ T μν - 3 ξ R[λμν]+ ξ ∇ σTμν . (1.37)

Page 12, Eq. (1.53): the coefficiens of the second and third terms were wrong:

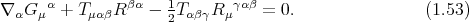
∇ αG μα + TμαβR βα - 1TαβγR μγαβ = 0. (1.53) 2

(Thanks to Gregory Giecold for this one).

Page 14, first line after Eq. (1.69): the subindex a should be a superindex:

We can immediately define the dual basis of 1-forms {e^a = e^a_μdx^μ} defined by...

Page 15, second line after Eq. (1.76): A non-holonomic... should be A holonomic

Page 16, Eq. (1.78): the indices of the last term were messed up:

[ ] ω ′c = Λc ω d( Λ-1)f - (Λ -1)d ∂ Λc (Λ -1)e . (1.78 ) ab d ef b b e d a

(Thanks to Gregory Giecold for this one).

Page 16, Eq. (1.84): the index b should be carried by the Vielbein:

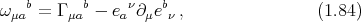
b b ν b ωμa = Γ μa - ea ∂μe ν , (1.84)

(Thanks to Masoud Soroush).

Page 20, Eq. (1.107): the sign after the first = should be +:

Lkg μν = 2∇ (μkν) = 0 , (1.107 )

Addendum: Eq. (1.108) in page 21 can be obtained as follows: from the Killing equation we have

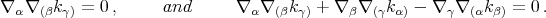
∇ α∇ (βkγ) = 0 , and ∇ α ∇(βkγ) + ∇ β∇ (γkα) - ∇ γ∇ (αk β) = 0 .

The last equation can be rewritten in the form

∇ ∇ k = - 1[∇ ,∇ ]k - 1[∇ ,∇ ]k , (α β) γ 2 α γ β 2 β γ α

and, using the Ricci identities for the l.h.s.

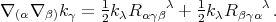
∇ (α ∇β)kγ = 1kλR αγβλ + 1kλR βγα λ. 2 2

Now, using the Bianchi identities for the metric-compatible torsinless curvature we get

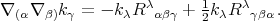
∇ (α∇ β)kγ = - kλR λαβγ + 1kλR λγβα. 2

Combining this equation with the Ricci identity

1 λ 1 λ ∇ [α ∇β]kγ = - 2kλR αβγ = 2 kλR γαβ ,

we get Eq. (1.108).

Page 21, Eq. (1.109): the sign after the first = should be +:

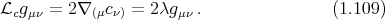
Lcg μν = 2∇ (μcν) = 2λgμν . (1.109 )

Page 21, Eq. (1.110): the sign after the first = should be +.

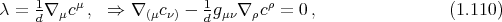
1 μ 1 ρ λ = d∇ μc , ⇒ ∇ (μcν) - dg μν∇ρc = 0 , (1.110)

Page 21, Eq. (1.115): the second left bracket [ in the subindices should be removed: all of them are antisymmetrized:

ρ⋅⋅⋅ρ σ σ g 1 (d-n)σ1⋅⋅⋅σ(d-n) = g[ρ1 1 ⋅⋅⋅g ρ(d-n)] (d-n) | | | gρ σ1 ⋅⋅⋅ gρ σ(d-n) | || 1 1 || (1.115) = --1-- || . . . || (d-n)!| .. .. .. | ||g σ1 ⋅⋅⋅ g σ(d-n)|| ρ(d- n) ρ(d-n)

Page 22, fourth line after Eq. (1.120): the right antisymmetrization bracket ] is missing after the last subindex (all of them are antisymmetrized):

Another important case is when k = p + 2 and F_(k) is the field-strength of the potential A_(p+1), so F_{(p+2)μ₁μ_(p+2)} = (p + 2)∂_[μ₁A_{(p+1)μ₂μ_(p+2)]}.

Page 23, first equation (unnumbered): d should eb replaced by p

⋆Fμ ⋅⋅⋅μ = (˜p + 2)∂[μ ˜A(˜p+1)μ⋅⋅⋅μ ]. 1 (˜p+2) 1 2 (˜p+2)

Page 23: the asterisk in the second line should be a star:

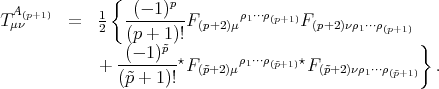
A { (- 1)p Tμν(p+1) = 12 --------F(p+2)μρ1⋅⋅⋅ρ(p+1)F (p+2)νρ1⋅⋅⋅ρ(p+1) (p + 1˜p)! } + -(--1)--⋆F ρ1⋅⋅⋅ρ(˜p+1)⋆F . (p˜+ 1)! (˜p+2)μ (˜p+2)νρ1⋅⋅⋅ρ(˜p+1)

(Thanks to Diego Blas)

Page 24, second line after Eq. (1.138): d - n - 1 should be d - n + 1 as in Eq. (1.139):

We can also take the divergence of the tensor and contract it with the volume element d^d-n+1Σ_{μ₁μ_n-1}.

Page 25, Eqs. (1.144): the order and position of the indices μ,ν,a,b in the curvature should be changed in the first equation, to coincide with Eq. (1.81) in the general case (not necessarily metric-compatible connection):

Rab = 1R μνabdxμ ∧ dxν = dωab - ωac ∧ ωcb. (1.144) 2

Addendum: The above equation is the second structure equation (the first is (1.143)), and they are valid for generic connections (non-metric compatible, torsionful) satisfying the first Vielbein postulate, which is equivalent to the first structure equation. Taking exterior derivatives of these two structure equations, and using d² = 0 plus the structure equations themselves one recovers the Bianchi identities Eqs. (1.30).

Chapter 1Differential Geometry

Chapter 1
Differential Geometry